拟合优度与t检验区别

1、 null

2、 差异如下：

3、 拟合优度检验用于评估整个模型的准确性。以模型 y = 10m + 2n 为例，通过比较真实观测值 y 与根据该模型输入变量（m, n）计算出的预测值 y*，利用统计量 R 衡量模型预测结果与实际数据之间的吻合程度，反映模型的整体拟合效果。

4、 若结果显著，表明系数10或2不为零；若不显著，则说明其可能为零，意味着对应变量在模型中影响不大。例如，若10接近零，可考虑将变量m从模型中剔除。

5、 请留意以下要点

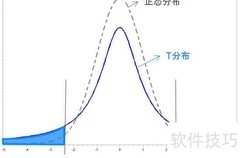
6、 选用检验方法时需满足其适用条件。t检验要求数据来自正态分布总体，样本为随机抽取，且进行均数比较时两组总体方差相等，即方差齐性。理论上，即使样本量较小，只要每组数据服从正态分布，且两组方差相近，仍可进行t检验。因此，应用前应充分验证前提条件是否成立。

7、 可通过观察数据分布或实施正态性检验来判断数据是否符合正态分布。对于方差齐性假设，可采用F检验或更具稳健性的Levenes检验。若上述条件未能满足，建议使用校正后的t检验，或改用非参数方法进行两组均值差异的比较，以提高分析结果的可靠性。

8、 单侧检验与双侧检验的主要区别在于拒绝域的设定。单侧检验的临界值较小，更容易拒绝原假设，因而第Ⅰ类错误概率较高。t检验中的p值表示在假设两均值无差异时，实际观测到差异或更大差异出现的概率。当总体真实无差异时，若p值过小而拒绝假设，则可能犯错。

9、 有学者主张当差异具有明确方向性时，可采用单侧检验，将t检验的P值除以二；另一些学者则坚持在任何情况下都应报告标准的双侧t检验结果。

10、 假设检验的结果不宜绝对化。当统计量落入临界域时，结果具有统计显著性，可拒绝原假设；若落在接受域，则结果不显著，应保留原假设。然而，不显著并不等于原假设成立，可能因样本量不足或出现第Ⅰ类错误所致，需结合实际情况审慎判断。