解方程：3.3x+2x-5x=6.6

一元一次方程是仅含一个未知数、次数为1且两边均为整式的等式。

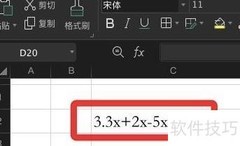
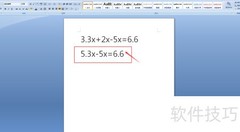
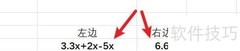
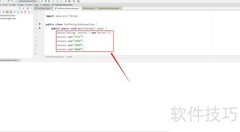
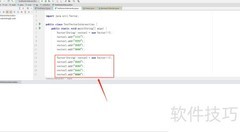
1、 解方程3.3x＋2x－5x＝6.6，合并同类项得0.3x＝6.6，解得x＝22。

2、 含有未知数的等式称为方程，若方程中仅含一个不为零的未知数，且该未知数的最高次数为1，并以整式形式呈现，则称为一元一次方程。这类方程的历史可追溯至约公元前1600年的古埃及，是人类早期数学的重要成果。公元820年前后，数学家花拉子米在其著作对消与还原中系统阐述了合并同类项和移项等解方程的基本方法，奠定了相关理论基础。到了16世纪，韦达发展出符号代数体系，进一步提出移项与同除的运算规则，推动了方程理论的发展。直至1859年，中国数学家李善兰首次将此类方程正式翻译为一元一次方程，这一名称沿用至今，成为现代数学中的基本概念之一。